day20 题目:剑指 Offer 07. 重建二叉树、剑指 Offer 16. 数值的整数次方、剑指 Offer 33. 二叉搜索树的后序遍历序列
知识点:树、递归、分治,难度为中等、中等、中等
学习计划链接:「剑指 Offer」 - 学习计划
| 题目 | 知识点 | 难度 |
|---|---|---|
| 剑指 Offer 07. 重建二叉树 | 树、数组、哈希表、分治 | 中等 |
| 剑指 Offer 16. 数值的整数次方 | 递归、数学 | 中等 |
| 剑指 Offer 33. 二叉搜索树的后序遍历序列 | 栈、树、二叉搜索树、递归 | 中等 |
剑指 Offer 07. 重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:
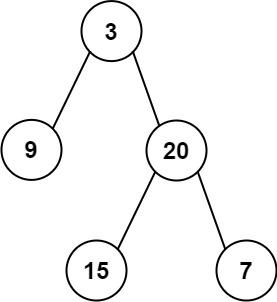
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]示例 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]限制:
0 <= 节点个数 <= 5000
思路及代码
冲刺春招-精选笔面试 66 题大通关 day9 同款题目 因为无重复,所以找出根节点在中序遍历中的下标,算出左右子节点数量,切分递归构建即可。
/**
* @param {number[]} preorder
* @param {number[]} inorder
* @return {TreeNode}
*/
var buildTree = function (preorder, inorder) {
if (preorder.length === 0) return null;
let root = new TreeNode(preorder[0]);
let index = inorder.indexOf(preorder[0]);
root.left = buildTree(preorder.slice(1, index + 1), inorder.slice(0, index));
root.right = buildTree(preorder.slice(index + 1), inorder.slice(index + 1));
return root;
};剑指 Offer 16. 数值的整数次方
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn)。不得使用库函数,同时不需要考虑大数问题。
示例 1:
输入: x = 2.00000, n = 10
输出: 1024.00000示例 2:
输入: x = 2.10000, n = 3
输出: 9.26100示例 3:
输入: x = 2.00000, n = -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25提示:
-100.0 < x < 100.0-2^31 <= n <= 2^31-1-10^4 <= xn <= 10^4
注意:本题与主站 50 题相同:https://leetcode-cn.com/problems/powx-n/
思路及代码
快速幂板子题,就是稍微注意下,踩了个坑,JS 中右移符号>>是算术移位,需要考虑符号位,而这里应该用>>> 逻辑右移,详见javascript 解决问题移位运算的坑
/**
* @param {number} x
* @param {number} n
* @return {number}
*/
var myPow = function (x, n) {
// 快速幂嘛。处理下n为负数的情况
function qpow(x, n) {
if (x == 1) return 1;
let res = 1;
while (n) {
if (n & 1) res *= x;
x *= x;
n >>>= 1;
}
return res;
}
return n < 0 ? 1 / qpow(x, -n) : qpow(x, n);
};剑指 Offer 33. 二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5
/ \
2 6
/ \
1 3示例 1:
输入: [1,6,3,2,5]
输出: false示例 2:
输入: [1,3,2,6,5]
输出: true提示:
数组长度 <= 1000
思路及代码
/**
* @param {number[]} postorder
* @return {boolean}
*/
var verifyPostorder = function (postorder) {
// 小大中间
function verify(l, r) {
if (l >= r) return true;
let root = postorder[r];
let leftRT = l;
// 小 找到第一个大的 实际左子树的根为leftRT-1
while (postorder[leftRT] < root) ++leftRT;
let rightRT = leftRT;
// 大 找到第一个小的 按理说会找到root的位置。
while (postorder[rightRT] > root) rightRT++;
return rightRT == r && verify(l, leftRT - 1) && verify(leftRT, r - 1);
// 验证左右子树
}
return verify(0, postorder.length - 1);
};